Cuando estudias informática te das cuenta de que hay cosas que tu haces que el resto del mundo no suele hacer y por lo que te llamarian friki generalmente, hoy me ha ocurrido una de esas cosas, tuve que escribir un programa para una practica:
- Currito Programador: Un programa en un lenguaje orientado a objetos
- Programador de Verdad: Un programa en C?
- Programador de verdad intentando que las cosas vayan rapido: Ensamblador
- Ingeniero: Programando con 1's y 0's para el Microprocesador que has diseñado tu mismo!
Aqui el programa que calcula Fibonacci del numero que esté en la primera direccion de memoria de datos y luego comprueba si es primo:
01100100000000010000000000000000
11001100000000000001000000000001
10110000000000110000000000000001
11001100000000000010100000000001
10001000101000010000000000000110
11001100000000110010000000000001
11001100011000100001100000000001
11001100000001000001000000000001
10110000101001010000000000000001
10000100101000110000000000000000
11001000000000000000000000000100
11001100011000000000100000000001
10110000101010100000000000000001
10110000000001000000000000000010
10110000000001110000000000000001
11001100001000000001000000000001
11001100000001000001100000000001
10001000001001000000000000001001
10001000010000000000000000001000
11001100001000000001000000000001
11001100000001000001100000000001
11001100010000110010100000001010
10001000101001110000000000000100
11001100010000110001000000000010
11001000000000000000000000010101
10110000100001000000000000000001
11001000000000000000000000001111
11001100000000100011000000001010
10000101010001100000000000000000
Despues de un duro dia solo queda decir: ¡Mi Cerebro va a estallar!
12.11.08
3.11.08
Cifras Monoalfabéticas
Una cifra monoalfabética es aquella en la que una letra de un alfabeto es cifrada por la misma letra, se puede representar una cifra monoalfabética escribiendo el alfabeto origen y el destino en una tabla:
Aunque la mayoria de cifras se realiza sobre el mismo alfabeto no tiene por que ser asi, podriamos cifrar cada letra por un caracter chino y seguiria siendo una cifra monoalfabética.
De esta forma podemos obtener un numero de cifras enorme, en concreto 26!
Cifras Afines
Para cifrar usando un ordenador representamos las letras como números, así seria a=1, b=2, ..., z=0, así las cifras aditivas serian una suma a estas letras, en este caso un desplazamiento de s posiciones (s mod 26).
Pasos:
Para la cifra multiplicativa tenemos que multiplicar el numero correspondiente a la letra por un número t, esto de nuevo puede ser mayor que 25 por lo que el resultado será el resto de dividirlo por 26 (aplicar mod 26).
Por ejemplo la cifra multiplicativa 2 seria:
Aquí tenemos un problema, ya que las letras de la cifra estan repetidas no podriamos recuperar el texto original por lo que esta cifra no se puede utilizar.
Que pasa con la cifra multiplicativa 3:
En este caso encontramos una cifra monoalfabética que si podemos usar, el caso es que son cifras monoalfabéticas: 1,3,5,7,9,11,15,17,19,21,23,25, esto hace un "gran total" de solo 12 cifras multiplicativas, lo que no es mucho aunque de todas formas se pueden combinar con las cifras aditivas.
A una letra de texto claro le sumamos un numero s y a este resultado lo multiplicamos por t, esto se escribe [s,t] y es lo que se llama una cifra afín, de este tipo hay 12x26 = 312 posibles cifras afines.
Aunque la mayoria de cifras se realiza sobre el mismo alfabeto no tiene por que ser asi, podriamos cifrar cada letra por un caracter chino y seguiria siendo una cifra monoalfabética.De esta forma podemos obtener un numero de cifras enorme, en concreto 26!
Cifras Afines
Para cifrar usando un ordenador representamos las letras como números, así seria a=1, b=2, ..., z=0, así las cifras aditivas serian una suma a estas letras, en este caso un desplazamiento de s posiciones (s mod 26).
Pasos:
- Se codifica la letra en un numero
- Se aplica el desplazamiento de s posiciones
- Si el resultado es mayor de 25 nos quedamos con el resto de dividirlo por 26.
- 'v' = 22
- 22 + 5 = 27
- 27 mod 25 = 1 = 'A'
Para la cifra multiplicativa tenemos que multiplicar el numero correspondiente a la letra por un número t, esto de nuevo puede ser mayor que 25 por lo que el resultado será el resto de dividirlo por 26 (aplicar mod 26).
Por ejemplo la cifra multiplicativa 2 seria:
Aquí tenemos un problema, ya que las letras de la cifra estan repetidas no podriamos recuperar el texto original por lo que esta cifra no se puede utilizar.Que pasa con la cifra multiplicativa 3:
En este caso encontramos una cifra monoalfabética que si podemos usar, el caso es que son cifras monoalfabéticas: 1,3,5,7,9,11,15,17,19,21,23,25, esto hace un "gran total" de solo 12 cifras multiplicativas, lo que no es mucho aunque de todas formas se pueden combinar con las cifras aditivas.
A una letra de texto claro le sumamos un numero s y a este resultado lo multiplicamos por t, esto se escribe [s,t] y es lo que se llama una cifra afín, de este tipo hay 12x26 = 312 posibles cifras afines.
31.10.08
Criptoanalisis (I)
Imaginamos ahora que estamos en el lado del malo, por esas cosas de la vida nos hemos enterado de que el texto cifrado con el que nos hemos encontrado ha sido cifrado mediante una cifra aditiva, hay dos formas principales con las que nos podemos enfrentar con el problema:
1) Ataque de fuerza bruta o (Exhaustión de todas las posibilidades):
Solo hay 26 posibles claves, asi que si las aplicamos todas habra un texto que tendra sentido, la razon de que esto funciona es que la mayoria de las combinaciones de letras no tienen sentido, el problema es que probar si un texto "tiene sentido" no es algo que podamos automatizar mediante un programa, o por lo menos tendriamos que tener un programa que conozca muchas palabras por lo que sería matar moscas a cañonazos.
IOL GYMMUAY XIYM HIN LYGUCH MYWLYN
Si aplicamos el razonamiento solo a la palabra HIN vemos que usando un desplazamiento 6 obtenemos la palabra "not" la unica que tiene sentido.
Ejemplo sacado de Cryptology
2) Análisis estadístico
En casi todos los lenguajes las letras del alfabeto no aparecen con la misma frecuencia y es curioso lo poco que cambian estas distribuciones entre distintos textos aunque si cambian entre diferentes idiomas.
Wikipedia Español
H4ck1t
Si ciframos un texto y le aplicamos un análisis estadistico veremos que la frecuencia de aparición de ciertas letras será similar a las originales a las que representan, en el ejemplo anterior tenemos:
Como la letra con mas apariciones es la Y, asumimos que representa a la "e" (que es la letra mas común en Ingles), esto hay que comprobarlo ya que está basado en estadísticas, siempre podríamos encontrarnos con un texto que hable de "Pañales dañados en España" y la ñ ocuparia una posición que no le corresponde. La evidencia la encontrámos en que las siguientes letras "Y" y "Z" tienen poca frecuencia al igual que la "f" y la "g" en el inglés.
La buena noticia es que esto es facil de automatizar, la mala es que al ser un método estadistico podemos fallar al hacer ciertas suposiciones y hay que tener cuidado con lo que suponemos, sobre todo en textos cortos.
(Ahora se para que sirve la estadistica que me enseñaron en la universidad)
1) Ataque de fuerza bruta o (Exhaustión de todas las posibilidades):
Solo hay 26 posibles claves, asi que si las aplicamos todas habra un texto que tendra sentido, la razon de que esto funciona es que la mayoria de las combinaciones de letras no tienen sentido, el problema es que probar si un texto "tiene sentido" no es algo que podamos automatizar mediante un programa, o por lo menos tendriamos que tener un programa que conozca muchas palabras por lo que sería matar moscas a cañonazos.
IOL GYMMUAY XIYM HIN LYGUCH MYWLYN
Si aplicamos el razonamiento solo a la palabra HIN vemos que usando un desplazamiento 6 obtenemos la palabra "not" la unica que tiene sentido.
Ejemplo sacado de Cryptology
2) Análisis estadístico
En casi todos los lenguajes las letras del alfabeto no aparecen con la misma frecuencia y es curioso lo poco que cambian estas distribuciones entre distintos textos aunque si cambian entre diferentes idiomas.
Wikipedia Español
H4ck1t
Si ciframos un texto y le aplicamos un análisis estadistico veremos que la frecuencia de aparición de ciertas letras será similar a las originales a las que representan, en el ejemplo anterior tenemos:
Como la letra con mas apariciones es la Y, asumimos que representa a la "e" (que es la letra mas común en Ingles), esto hay que comprobarlo ya que está basado en estadísticas, siempre podríamos encontrarnos con un texto que hable de "Pañales dañados en España" y la ñ ocuparia una posición que no le corresponde. La evidencia la encontrámos en que las siguientes letras "Y" y "Z" tienen poca frecuencia al igual que la "f" y la "g" en el inglés.La buena noticia es que esto es facil de automatizar, la mala es que al ser un método estadistico podemos fallar al hacer ciertas suposiciones y hay que tener cuidado con lo que suponemos, sobre todo en textos cortos.
(Ahora se para que sirve la estadistica que me enseñaron en la universidad)
Cifras Aditivas
Uno de los primeros usuarios de los que se tiene noticia de las cifras aditivas fue Cayo Julio Cesar (100-44 a.c), la cifra de cesar consistía en sumar tres posiciones a cada letra:
Texto Claro: ABCDEFGHIJKLMNOPQRSTUVWXYZ
Texto Cifrado: DEFGHIJKLMNOPQRSTUVWXYZABC
Se encripta substituyendo las letras que se encuentran en el texto en claro por las del cifrado, así cifra se convierte en FLIUD, para descifrar se restan tres posiciones a cada letra. Hay 26 posibles claves que se pueden usar con este método que serian las posiciones a desplazar en nuestro alfabeto.
Cifrar con las tablas de arriba es fácil pero tedioso para textos largos, así que en 1470 el arquitecto Leone Battista Alberti inventó una maquina hecha con dos discos que mecanizaba el proceso, el disco interior podía rotar generando la cifra aditiva.
El algoritmo y la clave tienen funciones diferentes, el algoritmo es grande y complicado, en consecuencia no se debe mantener en secreto, la seguridad del algoritmo debe recaer en la clave.
Texto Claro: ABCDEFGHIJKLMNOPQRSTUVWXYZ
Texto Cifrado: DEFGHIJKLMNOPQRSTUVWXYZABC
Se encripta substituyendo las letras que se encuentran en el texto en claro por las del cifrado, así cifra se convierte en FLIUD, para descifrar se restan tres posiciones a cada letra. Hay 26 posibles claves que se pueden usar con este método que serian las posiciones a desplazar en nuestro alfabeto.
Cifrar con las tablas de arriba es fácil pero tedioso para textos largos, así que en 1470 el arquitecto Leone Battista Alberti inventó una maquina hecha con dos discos que mecanizaba el proceso, el disco interior podía rotar generando la cifra aditiva.
El algoritmo y la clave tienen funciones diferentes, el algoritmo es grande y complicado, en consecuencia no se debe mantener en secreto, la seguridad del algoritmo debe recaer en la clave.
26.10.08
La Scitala Espartana
Todo viene de hace 2500 años, por lo menos segun lo cuenta Plutarco, el gobierno de Esparta enviaba mensajes secretos a sus generales usando un curioso método, la idea era que emisor y receptor tenian un cilindro cada uno de el mismo radio en el que el emisor enrollaba una tira de tela y escribia sobre la tira en sentido horizontal. Asi quedaba oculto el mensaje que se enviaba y solo se podia recuperar si se disponia de un cilindro igual al que tenia el emisor.
La Scitala usada tiene una circunferencia c, que se puede medir en número de letras, asi que lo que hay que descubrir el la circunferencia.
Para el siguiente mensaje:
SYBLCRESEERACHTAYPUOHIPHRUEMTYILSOO!TDOFG
c=5
S R R A H U I ! G
Y E A Y I E L T
B S C P P M S D
L E H U H T O O
C E T O R Y O F
c=6
S E C U R I T
Y S H O U L D
B E T H E S O
L E A I M O F
C R Y P T O G
R A P H Y !
La Scitala es un metodo de cifra por transposición, las letras permanecen iguales y el cambio se produce en la posicion, este método (transposición) se sigue usando combinado con otros como la substitucion.
Para saber mas:
Wikipedia
27.9.08
Con que juegan los niños
Ayer andando por un gran centro comercial (de esos que han llenado Madrid) me encontre con algunos juguetes que son cuanto menos curiosos.
La discusion previa en el departamento de marteking habra sido algo como lo siguiente:
x) Lo importante es que sea sorpresa para los niños que muñeco va a ir en cada caja.
o) Entonces los tapamos completamente?
x) No, no. Necesitamos que se vea algo para que sea un aliciente para el niño pedir el juguete.
o) Ajam ... Ya tengo la solución.
También conocidos como "Los muñecos terroristas", "Los muñecos muyaidines", "La yihad de los pañales"
Disclaimer: Esto es una broma, unos muñecos que nos hicieron gracia y no pretende atentar contra la salud mental de ninguna persona religiosa.
La discusion previa en el departamento de marteking habra sido algo como lo siguiente:
x) Lo importante es que sea sorpresa para los niños que muñeco va a ir en cada caja.
o) Entonces los tapamos completamente?
x) No, no. Necesitamos que se vea algo para que sea un aliciente para el niño pedir el juguete.
o) Ajam ... Ya tengo la solución.
También conocidos como "Los muñecos terroristas", "Los muñecos muyaidines", "La yihad de los pañales"
Disclaimer: Esto es una broma, unos muñecos que nos hicieron gracia y no pretende atentar contra la salud mental de ninguna persona religiosa.
15.9.08
Los ingenieros
Los ingenieros son una especie de seres humanos
También tienen gusto por ciertas bromas ... macabras por decirlo de alguna manera, por ejemplo en el MIT (cuna de muchos grandes Ingenieros) han realizado bromas tan espectaculares como subir un camión sobre la cúpula llamada allí Great Dome tal como se ve en las fotos:
y algunas otras barbaridades contadas en el blog de Fogonazos
Yo nunca he hecho barbaridades tan grandes alguna pequeñita si pero ... mmm ahora que soy ingeniero tengo que pensar alguna cosa para hacer!!!
Guajajaja
También tienen gusto por ciertas bromas ... macabras por decirlo de alguna manera, por ejemplo en el MIT (cuna de muchos grandes Ingenieros) han realizado bromas tan espectaculares como subir un camión sobre la cúpula llamada allí Great Dome tal como se ve en las fotos:
y algunas otras barbaridades contadas en el blog de Fogonazos
Yo nunca he hecho barbaridades tan grandes alguna pequeñita si pero ... mmm ahora que soy ingeniero tengo que pensar alguna cosa para hacer!!!
Guajajaja
28.7.08
Matematicas de servilleta (El Seno)
De vez en cuando alguien me pide que le explique cosas y por alguna u otra razón al explicarlas en un trozo de papel (o servilleta en un bar) se entienden mejor, así que he pensado, "por que no pegar directamente el trozo de servilleta?", total se entiende mejor y le da una pinta de cutre que ayuda a quitar miga al asunto. Como primera entrega: El seno de un angulo agudo.
9.5.08
Porcentajes de acierto
He hecho un modulo nuevo que mide los porcentajes de acierto del filtro con respecto del video, la forma de acierto se corresponde con el numero de pixels del objeto que se encuentran en la zona pronosticada por el filtro, de este modo si el objeto tiene 1600 pixels y dentro de la zona caen los 1600 pixels el acierto sera del 100%.
Existe el problema de que cuando el objeto está perdido la zona pronosticada por el filtro va creciendo, debido a la perdida de confianza en la prediccion, aun asi si el objeto entero esta dentro de dicha zona el acierto sera del 100%, lo que no parece muy logico.
Hay que buscar una formula que tenga en cuenta que estadisticamente existe una posibilidad de que el objeto caiga en una zona de la pantalla que crece proporcionalmente a la zona de la pantalla observada y sustraer dicha probabilidad de nuestro calculo.
8.5.08
Haciendo diagramas
Para hacer un proyecto medianamente grande hacen falta muchos diagramas, aunque en principio estaban casi todos en papel los he ido pasando usando Dia.
Como se ve cada modulo salvo el historial tiene su modulo de pruebas que ha sido usado durante la creación del modulo para probar su funcionamiento.
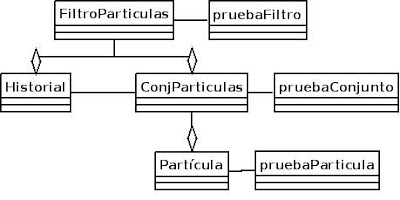En este diagrama se ven las funciones y atributos importantes de cada clase omitiendo los de las clases de pruebas ya que una vez creado el modulo y probado no influyen mas en el software creado.
Continuo con la memoria.
Como se ve cada modulo salvo el historial tiene su modulo de pruebas que ha sido usado durante la creación del modulo para probar su funcionamiento.
En este diagrama se ven las funciones y atributos importantes de cada clase omitiendo los de las clases de pruebas ya que una vez creado el modulo y probado no influyen mas en el software creado.
Continuo con la memoria.
8.4.08
Porque la interpolación no fue una buena idea
Mientras que estamos interpolando la cosa va bien y la operacion es bastante precisa, pero en nuestro problema en general no necesitamos interpolar nada sino extrapolar, es decir que tenemos que averiguar que pasara en el futuro.
Esto es bastante mas dificil de lo que parece por muchas razones, la primera y mas antiintuitiva es que no se puede interpolar directamente y en funcion de x ya que tampoco tenemos estimacion de como crece x asi que nos quedan dos opciones:
interpolar x e y en funcion de t (por ejemplo el numero del frame en que estamos).
interpolar x en funcion de t e y en funcion de x.
Esto no es demasiado problema pero vamos perdiendo precision. El verdadero problema es que el polinomio se ajusta muy bien entre los n puntos que le damos, sin embargo predecir lo que hara la funcion a partir de ahi no es facil.
Algunos ejemplos:
En la zona en que se interpola las funciones coinciden, pero luego el polinomio crece mucho mas rápido por lo que la estimación es cada vez peor.
Para esta línea la estimación es casi perfecta, pero para conseguir esto fue necesario probar diferentes separaciones entre puntos y grados del polinomio, este en concreto tiene grado 4 y los puntos han sido tomados cada 5t.
Este es un caso extremadamente malo en que la funcion de estimacion crece de forma exponencial a diferencia de la original que es lineal.
Otro ejemplo de funciones que crecen a diferente velocidad.
Lo importante a darse cuenta es que dependemos de los puntos tomados, la separación entre ellos, la función original y el grado del polinomio usado y los parámetros que son buenos para una función original no lo son para otra, de modo que tendríamos que dejar al programa que decida, esto es un montón de trabajo y computo.
La idea ahora es usar algún tipo de componente derivativa dentro de la dinámica inercial para suplir esto que nos ayude a seguir objetos en trayectoria curva y no complique excesivamente las cosas para aquellos que siguen una recta.
Esto es bastante mas dificil de lo que parece por muchas razones, la primera y mas antiintuitiva es que no se puede interpolar directamente y en funcion de x ya que tampoco tenemos estimacion de como crece x asi que nos quedan dos opciones:
interpolar x e y en funcion de t (por ejemplo el numero del frame en que estamos).
interpolar x en funcion de t e y en funcion de x.
Esto no es demasiado problema pero vamos perdiendo precision. El verdadero problema es que el polinomio se ajusta muy bien entre los n puntos que le damos, sin embargo predecir lo que hara la funcion a partir de ahi no es facil.
Algunos ejemplos:
En la zona en que se interpola las funciones coinciden, pero luego el polinomio crece mucho mas rápido por lo que la estimación es cada vez peor.
Para esta línea la estimación es casi perfecta, pero para conseguir esto fue necesario probar diferentes separaciones entre puntos y grados del polinomio, este en concreto tiene grado 4 y los puntos han sido tomados cada 5t.
Este es un caso extremadamente malo en que la funcion de estimacion crece de forma exponencial a diferencia de la original que es lineal.
Otro ejemplo de funciones que crecen a diferente velocidad.Lo importante a darse cuenta es que dependemos de los puntos tomados, la separación entre ellos, la función original y el grado del polinomio usado y los parámetros que son buenos para una función original no lo son para otra, de modo que tendríamos que dejar al programa que decida, esto es un montón de trabajo y computo.
La idea ahora es usar algún tipo de componente derivativa dentro de la dinámica inercial para suplir esto que nos ayude a seguir objetos en trayectoria curva y no complique excesivamente las cosas para aquellos que siguen una recta.
2.4.08
Incertidumbre
Cuando se pierde de vista un objeto podemos hacer predicciones a cerca de donde esta, pero lo cierto es que nuestra incertidumbre aumenta con el tiempo que lleva el objeto fuera de nuestro alcance y hay que representarlo de alguna manera.
Si estamos trabajando en periodos de tiempo discretos
lo mas fácil es poner la incertidumbre en función del tiempo, pero como lo que queremos hacer es representarlo mas gráficamente puede que se nos ocurra por ejemplo aumentar el tamaño del centroide de la estimación en uno por cada instante t que lleve perdido.
Supongamos que el centroide es un cuadrado, y que es de lado 40, esto implica que si perdemos nuestro objeto durante 40 instantes de tiempo el cuadrado sera el doble de grande (cubrirá 4 veces mas área).
Lo cierto es que no sabemos en general a que velocidad estamos perdiendo precisión por lo que tenemos que comprobarlo experimentalmente, después de unas cuantas pruebas he obtenido que si aumento el tamaño del cuadrado en proporción 2:1 con respecto al tiempo que lleva el objeto perdido se consiguen resultados aceptables.
También he inicializado el generador de pseudoaletorios con srand(time(NULL)) de modo que ahora cada repetición es diferente de las anteriores.
Si estamos trabajando en periodos de tiempo discretos
Supongamos que el centroide es un cuadrado, y que es de lado 40, esto implica que si perdemos nuestro objeto durante 40 instantes de tiempo el cuadrado sera el doble de grande (cubrirá 4 veces mas área).
Lo cierto es que no sabemos en general a que velocidad estamos perdiendo precisión por lo que tenemos que comprobarlo experimentalmente, después de unas cuantas pruebas he obtenido que si aumento el tamaño del cuadrado en proporción 2:1 con respecto al tiempo que lleva el objeto perdido se consiguen resultados aceptables.
También he inicializado el generador de pseudoaletorios con srand(time(NULL)) de modo que ahora cada repetición es diferente de las anteriores.
27.3.08
Interpolación (3)
La idea que proponen en numerical recipes para la interpolación de Lagrange es bastante mejor, la idea es definir:
como el valor x del unico polinomio de grado 0 (una constante) que pasa por 
, entonces 
, definimos de la misma forma 
y de forma analoga diremos que 
como el valor en x del unico polinomio de grado 1 (una recta) que pasa a la vez por y 
, seguimos definiendo de esta forma todos los polinomios hasta el grado del polinomio de interpolacion que queramos, ya que el polinomio 
es el unico polinomio de grado N que pasa por todos los puntos que queremos!
Si ponemos los valores de P en una tabla en forma de "arbol" obtenemos lo siguiente:
El algoritmo para obtener hijos a partir de los ancestros de este arbol de llama algoritmo de Neville:
Esto funciona porque los "padres" ya están de acuerdo en
.
La siguiente mejora para la recursión es guardar un registro de las diferencias entre padres e hijos, esto es:
Para
Y juntando esto con la ecuacion de Neville obtenemos:
Para cada nivel m en nuestro arbol las Ces y las Des son las correcciones que hay que aplicar para convertir el polinomio en un orden mayor.
Finalmente obtenemos
, que es el resultado de 
mas los Ces y Des que haya en el camino en el árbol tomando siempre el hijo de la derecha.
Las ideas fueron sacadas de Numerical Recipes in C, que como siempre esta mucho mejor explicado que aquí y mucho mas en ingles.
Si ponemos los valores de P en una tabla en forma de "arbol" obtenemos lo siguiente:
El algoritmo para obtener hijos a partir de los ancestros de este arbol de llama algoritmo de Neville:
Esto funciona porque los "padres" ya están de acuerdo en
La siguiente mejora para la recursión es guardar un registro de las diferencias entre padres e hijos, esto es:
Para
Y juntando esto con la ecuacion de Neville obtenemos:
Para cada nivel m en nuestro arbol las Ces y las Des son las correcciones que hay que aplicar para convertir el polinomio en un orden mayor.
Finalmente obtenemos
Las ideas fueron sacadas de Numerical Recipes in C, que como siempre esta mucho mejor explicado que aquí y mucho mas en ingles.
26.3.08
Interpolación (2)
Entre dos puntos (diferentes) pasa una única línea, entre tres puntos (diferentes) pasa una única función cuadrática etc. etc.
El polinomio de Lagrange de grado N-1 nos da exactamente eso para N puntos tales que
, esto es:
La idea es que en los puntos
que nos dan todos los polinomios excepto uno serán 0, y el que no es cero nos dará justo el valor esperado.
Programar esto tal como viene no es una idea demasiado buena ya que tenemos una complejidad O(N²) por cada punto nuevo que queramos calcular.
El polinomio de Lagrange de grado N-1 nos da exactamente eso para N puntos tales que
La idea es que en los puntos
Programar esto tal como viene no es una idea demasiado buena ya que tenemos una complejidad O(N²) por cada punto nuevo que queramos calcular.
25.3.08
Interpolación (1)
A veces conocemos el valor de una función f(x) en unos puntos dados 
siendo 
pero no tenemos una expresión que nos permita calcular f(x) en otro punto cualquiera.
La misión es obtener una estimación de f(x) para un x cualquiera de modo que la curva que dibujemos sea "suave" entre los puntos y en su alrededor. La forma en que aproximemos las funciones tiene que ser general porque no sabemos en principio con que función nos estamos enfrentando. Las aproximaciones mas comunes o al menos las que aprendí en mis clases de calculo son (1)Polinomios (2)Cocientes de polinomios y (3)Funciones trigonométricas.
Hay funciones que tienen un "mal comportamiento" con la interpolación, para saber si el comportamiento ha sido bueno o malo es útil tener una estimación del error, hay que notar que estamos presumiendo que las funciones son suaves y continuas, lo que es perfecto para el movimiento real.
La idea básica es encontrar una función que encaje en los puntos dados y luego evaluarla para otro punto deseado, la mayoría de las aproximaciones empiezan con un punto y van haciendo correcciones al ir agregando otros nuevos puntos, esto nos da una complejidad de
La misión es obtener una estimación de f(x) para un x cualquiera de modo que la curva que dibujemos sea "suave" entre los puntos y en su alrededor. La forma en que aproximemos las funciones tiene que ser general porque no sabemos en principio con que función nos estamos enfrentando. Las aproximaciones mas comunes o al menos las que aprendí en mis clases de calculo son (1)Polinomios (2)Cocientes de polinomios y (3)Funciones trigonometricas.
Hay funciones que tienen un "mal comportamiento" con la interpolación, para saber si el comportamiento ha sido bueno o malo es útil tener una estimación del error, hay que notar que estamos presumiendo que las funciones son suaves y continuas, lo que es perfecto para el movimiento real.
La interpolación local con un numero finito de vecinos no es continua en las derivadas, si necesitamos que sea continua en las derivadas tenemos que usas la no localidad, por ejemplo con splines, es decir entre dos puntos dados definimos un polinomio que los interpola.
La misión es obtener una estimación de f(x) para un x cualquiera de modo que la curva que dibujemos sea "suave" entre los puntos y en su alrededor. La forma en que aproximemos las funciones tiene que ser general porque no sabemos en principio con que función nos estamos enfrentando. Las aproximaciones mas comunes o al menos las que aprendí en mis clases de calculo son (1)Polinomios (2)Cocientes de polinomios y (3)Funciones trigonométricas.
Hay funciones que tienen un "mal comportamiento" con la interpolación, para saber si el comportamiento ha sido bueno o malo es útil tener una estimación del error, hay que notar que estamos presumiendo que las funciones son suaves y continuas, lo que es perfecto para el movimiento real.
La idea básica es encontrar una función que encaje en los puntos dados y luego evaluarla para otro punto deseado, la mayoría de las aproximaciones empiezan con un punto y van haciendo correcciones al ir agregando otros nuevos puntos, esto nos da una complejidad de
La misión es obtener una estimación de f(x) para un x cualquiera de modo que la curva que dibujemos sea "suave" entre los puntos y en su alrededor. La forma en que aproximemos las funciones tiene que ser general porque no sabemos en principio con que función nos estamos enfrentando. Las aproximaciones mas comunes o al menos las que aprendí en mis clases de calculo son (1)Polinomios (2)Cocientes de polinomios y (3)Funciones trigonometricas.
Hay funciones que tienen un "mal comportamiento" con la interpolación, para saber si el comportamiento ha sido bueno o malo es útil tener una estimación del error, hay que notar que estamos presumiendo que las funciones son suaves y continuas, lo que es perfecto para el movimiento real.
La interpolación local con un numero finito de vecinos no es continua en las derivadas, si necesitamos que sea continua en las derivadas tenemos que usas la no localidad, por ejemplo con splines, es decir entre dos puntos dados definimos un polinomio que los interpola.
22.3.08
La aplicación que se cae
Todos hemos tenido alguna vez el problema de que una aplicación se cierra sin motivo aparente, y si esa aplicación es el emule/bittorrent/ares etc toca mucho la moral porque es tiempo que va a tardar de mas en descargar lo que sea, así que si pudiéramos darnos cuenta de que se ha caído y volverlo a poner solo unos minutos después seria una buena idea pero claro ... si no estas todo el día en frente del pc es complicado.
A menos que tengas un espía!, este es mi espía:
Luego añadimos la siguiente linea al cron:
0,15,30,45 * * * * $HOME/scripts/crash.sh
y ya esta, cada 15 minutos se comprobara si la aplicación esta funcionando y si no la volverá a lanzar.
NOTA: manda la salida del programa a la porra (/dev/null) y el log es cuuutre pero para mi sobra
A menos que tengas un espía!, este es mi espía:
#!/bin/bash
PID=$(pidof $APLICACION)
if [ "$PID" = "" ]
then
echo $(date +"%d %m %Y - %H:%M:%S") reiniciando aplicacion >> $HOME/crash.log
$APLICACION 2>&1 > /dev/null
fi
Luego añadimos la siguiente linea al cron:
0,15,30,45 * * * * $HOME/scripts/crash.sh
y ya esta, cada 15 minutos se comprobara si la aplicación esta funcionando y si no la volverá a lanzar.
NOTA: manda la salida del programa a la porra (/dev/null) y el log es cuuutre pero para mi sobra
17.3.08
Pequeñas Mejoras
A raíz de las ultimas pruebas descubrí algunos fallos, el mas evidente era el que perdiese a los objetos que se movían con una velocidad "no entera", para solucionarlo se me ocurrió agregar un acumulador de velocidad que funciona de la siguiente forma:
velxAcum=velx+velxAcum-(int)(trunc(velx+velxAcum));
velyAcum=vely+velyAcum-(int)(trunc(vely+velyAcum));
De forma que guarda la porción del movimiento que por no ser entera no se ha podido aplicar a un solo paso, pero que al sumarse con otras partes no enteras dara finalmente con una solución mejor que si las ignoramos.
Este es el resultado:
Los saltos que se observan son debido a que el centroide se calcula desde las partículas que se dispersan aleatoriamente. No esta mal teniendo en cuenta que el objeto es invisible al filtro durante 80 frames y aun así la estimación cae sobre el objeto :)
velxAcum=velx+velxAcum-(int)(trunc(velx+velxAcum));
velyAcum=vely+velyAcum-(int)(trunc(vely+velyAcum));
De forma que guarda la porción del movimiento que por no ser entera no se ha podido aplicar a un solo paso, pero que al sumarse con otras partes no enteras dara finalmente con una solución mejor que si las ignoramos.
Este es el resultado:
Los saltos que se observan son debido a que el centroide se calcula desde las partículas que se dispersan aleatoriamente. No esta mal teniendo en cuenta que el objeto es invisible al filtro durante 80 frames y aun así la estimación cae sobre el objeto :)
12.3.08
Probando el filtro
Finalmente solucione el problema del circulo y la espiral, la idea es que la x no tiene porque avanzar un pixel en cada iteración, así que la solución que se me ocurrió es rellenar los espacios en que la y avanza mas de un pixel interpolando de alguna forma los pasos intermedios en que la x estaría estática.
Una vez conseguido eso pasamos a las pruebas:
Prueba 1: El rectángulo
Valoración: Satisfactoria, el filtro hace exactamente lo que tiene que hacer y no pierde el objeto aunque "desaparezca", cuando el objeto está rojo el filtro no lo reconoce, esto ayuda a que se pueda evaluar el funcionamiento ya que yo si lo puedo ver (es un super poder que tengo).
Prueba 2: La Recta
Valoración: Mal, muy mal, lo he puesto a posta para que lo haga mal, el problema es que la ecuación de esta recta es y = 50 + 1.2x, dado que el filtro esta trabajando sobre cantidades discretas pierde ese 0.2 a cada iteración, por eso se retrasa, esta en mi lista de TODO arreglar ese aspecto del filtro.
Prueba 3: El Circulo
Valoración: Regular, el filtro funciona como era de esperar, el problema es que esto no es suficiente para seguir al objeto, sigue la recta perpendicular al circulo, esto no pasaría o mejoraría si usase de alguna forma la derivada de la función... esto aun son suposiciones.
Prueba 4: La Espiral
Valoración: Similar al circulo, este es solo un caso ligeramente mas general al del circulo pero quedaba bonito y ademas me gustan las espirales que pasa. Se ve en el video que en algunos casos funciona mejor que en otros, esto depende de la zona de la circunferencia en que nos encontremos ya que en las zonas que estan proximas a los ejes del plano se recorren pixeles sucesivos en una misma linea, es decir solo hay movimiento en el eje x o en el eje y pero no en ambos.
Prueba 5: La Mosca
Valoración: Este es el prototipo de caso en que la realimentación no funciona, ya que el movimiento cambia rápidamente de dirección de forma quasi-aleatoria. No se me ocurre ninguna forma de hacer que esto funcione así que de momento tendrá que esperar.
Prueba 6: Función Sinusoide
Valoración: En este caso existe el mismo problema que sobre la recta, dado que estamos aproximando reales con enteros tenemos el problema de perdida de precisión, aun así no esta mal como primera aproximación.
Una vez conseguido eso pasamos a las pruebas:
Prueba 1: El rectángulo
Valoración: Satisfactoria, el filtro hace exactamente lo que tiene que hacer y no pierde el objeto aunque "desaparezca", cuando el objeto está rojo el filtro no lo reconoce, esto ayuda a que se pueda evaluar el funcionamiento ya que yo si lo puedo ver (es un super poder que tengo).
Prueba 2: La Recta
Valoración: Mal, muy mal, lo he puesto a posta para que lo haga mal, el problema es que la ecuación de esta recta es y = 50 + 1.2x, dado que el filtro esta trabajando sobre cantidades discretas pierde ese 0.2 a cada iteración, por eso se retrasa, esta en mi lista de TODO arreglar ese aspecto del filtro.
Prueba 3: El Circulo
Valoración: Regular, el filtro funciona como era de esperar, el problema es que esto no es suficiente para seguir al objeto, sigue la recta perpendicular al circulo, esto no pasaría o mejoraría si usase de alguna forma la derivada de la función... esto aun son suposiciones.
Prueba 4: La Espiral
Valoración: Similar al circulo, este es solo un caso ligeramente mas general al del circulo pero quedaba bonito y ademas me gustan las espirales que pasa. Se ve en el video que en algunos casos funciona mejor que en otros, esto depende de la zona de la circunferencia en que nos encontremos ya que en las zonas que estan proximas a los ejes del plano se recorren pixeles sucesivos en una misma linea, es decir solo hay movimiento en el eje x o en el eje y pero no en ambos.
Prueba 5: La Mosca
Valoración: Este es el prototipo de caso en que la realimentación no funciona, ya que el movimiento cambia rápidamente de dirección de forma quasi-aleatoria. No se me ocurre ninguna forma de hacer que esto funcione así que de momento tendrá que esperar.
Prueba 6: Función Sinusoide
Valoración: En este caso existe el mismo problema que sobre la recta, dado que estamos aproximando reales con enteros tenemos el problema de perdida de precisión, aun así no esta mal como primera aproximación.
uuuuuuu
uu$$$$$$$$$$$uu
uu$$$$$$$$$$$$$$$$$uu
u$$$$$$$$$$$$$$$$$$$$$u
u$$$$$$$$$$$$$$$$$$$$$$$u
u$$$$$$$$$$$$$$$$$$$$$$$$$u
u$$$$$$$$$$$$$$$$$$$$$$$$$u
u$$$$$$" "$$$" "$$$$$$u
"$$$$" u$u $$$$"
$$$u u$u u$$$
$$$u u$$$u u$$$
"$$$$uu$$$ $$$uu$$$$"
"$$$$$$$" "$$$$$$$"
u$$$$$$$u$$$$$$$u
u$"$"$"$"$"$"$u
uuu $$u$ $ $ $ $u$$ uuu
u$$$$ $$$$$u$u$u$$$ u$$$$
$$$$$uu "$$$$$$$$$" uu$$$$$$
u$$$$$$$$$$$uu """"" uuuu$$$$$$$$$$
$$$$"""$$$$$$$$$$uuu uu$$$$$$$$$"""$$$"
""" ""$$$$$$$$$$$uu ""$"""
uuuu ""$$$$$$$$$$uuu
u$$$uuu$$$$$$$$$uu ""$$$$$$$$$$$uuu$$$
$$$$$$$$$$"""" ""$$$$$$$$$$$"
"$$$$$" ""$$$$""
$$$" $$$$"
7.3.08
Algo de Geometria I
Mi tarea de hoy ha sido programar pequeñas funciones en C++ que sean capaces de devolver coordenadas en pantalla que representen ciertas funciones.
Sen(x)
El problema con esta función es que esta definida entre -1 y 1, por lo que hace falta escalar la imagen y discretizarla.
y=a+(int)round(b*sin(gradosAradianes(i)));
Rectangulo:
Esta funcion es tan simple como concatenar 4 bucles que lo describan.
Circunferencia:
Al despejar la y obtenemos lo siguiente:
Esto debería generar un circulo pero como se puede comprobar no lo genera:
Esto se debe a que el avance de las x es constante cuando en realidad no tiene por que ser así, es decir que aunque describe un circulo correctamente hay zonas en que se mueve mas rápido de lo que cabria esperar debido al efecto de la discretización.
Algunas imágenes contienen oclusiones totales o cambios de color, esa característica se usara para probar el filtro.
Todas las gráficas fueron sacadas de la Wikipedia
Sen(x)
El problema con esta función es que esta definida entre -1 y 1, por lo que hace falta escalar la imagen y discretizarla.
y=a+(int)round(b*sin(gradosAradianes(i)));
Rectangulo:
Esta funcion es tan simple como concatenar 4 bucles que lo describan.Circunferencia:
Al despejar la y obtenemos lo siguiente:
Esto debería generar un circulo pero como se puede comprobar no lo genera:
Esto se debe a que el avance de las x es constante cuando en realidad no tiene por que ser así, es decir que aunque describe un circulo correctamente hay zonas en que se mueve mas rápido de lo que cabria esperar debido al efecto de la discretización.
Algunas imágenes contienen oclusiones totales o cambios de color, esa característica se usara para probar el filtro.
Todas las gráficas fueron sacadas de la Wikipedia
6.3.08
Diseño Modular
Después de muchas vueltas y mas vueltas me he decidido por un diseño para el nuevo sintetizador de vídeo mejorado (mágico, plus, maestro del universo!), la idea es que el usuario tenga que escribir un pequeño fichero describiendo el tipo de video que desea y se genere automáticamente.
Un ejemplo del fichero de usuario sería:
NFrames=340
Width=400
Height=400
FPS=1
ObjectSize=40
Function=/home/zenko/workspace/senoidal/Debug/senoidal
args=100 200 0 340
Color=/home/zenko/workspace/colores/Debug/colores
Sections=200 255 255 255 50 0 0 0 90 255 255 255
Donde cada cosa es exactamente lo que parece según la descripción.
Function es la ruta a un ejecutable que recibe 4 argumentos a, b, inicio y fin, con esto ejecuta la función:
for(i=primero;i < ultimo;i++)
{
y=a+b*sin(gradosAradianes(i)));
}
Color es la ruta de un ejecutable que devuelve ternas R G B y recibe n parámetros de tal forma que si dividimos los parámetros en grupos de 4 tenemos:
1) Numero de ternas
2) R
3) G
4) B
y nos devuelve una lista de N ternas.
Finalmente el script toma la salida de ambos programas y pega los ficheros en uno solo tal que guarde la sintaxis esperada por el generador.
#Numero de frames del vídeo
4
#Ancho del vídeo
400
#Alto del ideo
400
#FPS para el vídeo
1
#Tamaño del objeto
40
#x y R G B para cada frame
1 102 255 255 255
2 103 255 255 255
3 105 255 255 255
De esta forma cada vez que queramos generar un vídeo con una función extraña o exótica solo hará falta escribir la función y todo el resto del código sera reutilizable.
4.3.08
Sintetizador de video
Una vez conseguido el algoritmo básico de seguimiento se inicia la etapa de pruebas en donde necesitaré muchos vídeos de distintos tipos, es una buena practica tener un sintetizador que me cree vídeos a medida para comprobar el seguimiento.
En principio las funciones escogidas son:
a*Sen(x)+b
a*x+b
(x-h)^2 + (y-k)^2 = r^2
Espiral de Arquímedes
Esta será la primera batería de pruebas para comprobar el rendimiento del filtro.
Prueba usando 100*Sen(x)+200
El vídeo es bastaaaante lento, pero es parametrizable así que se puede poner a la velocidad deseada.
Falta escribir algunas de las funciones y modelizar las oclusiones, una vez conseguido esto necesito también alguna forma de tomar estadísticas del seguimiento del objeto.
En principio las funciones escogidas son:
a*Sen(x)+b
a*x+b
(x-h)^2 + (y-k)^2 = r^2
Espiral de Arquímedes
Esta será la primera batería de pruebas para comprobar el rendimiento del filtro.
Prueba usando 100*Sen(x)+200
El vídeo es bastaaaante lento, pero es parametrizable así que se puede poner a la velocidad deseada.
Falta escribir algunas de las funciones y modelizar las oclusiones, una vez conseguido esto necesito también alguna forma de tomar estadísticas del seguimiento del objeto.
29.2.08
Evitando la dispersion desde un centro
Un efecto extraño que teníamos en anteriores versiones es que la dispersión generaba un cuadrado casi perfecto, se debe a que las todas las partículas se dispersan desde un mismo centro, esto no es tan buena idea ya que se supone que estamos perdiendo precisión con respecto a cuando tenemos medida, y en ese momento la nube es mas dispersa.
Para solucionarlo he cambiado la forma en que se calcula la velocidad y los centroides, el centroide se sigue calculando a partir de las n partículas en vez de moverlo por la inercia, las partículas se dispersan con la función aleatoria estándar como de costumbre pero la velocidad no se actualiza de nuevo hasta obtener una nueva medida.
Esto que parece ser la idea mas lógica y obvia no se me ocurrió hasta tiempo después de estarlo pensando!
Para solucionarlo he cambiado la forma en que se calcula la velocidad y los centroides, el centroide se sigue calculando a partir de las n partículas en vez de moverlo por la inercia, las partículas se dispersan con la función aleatoria estándar como de costumbre pero la velocidad no se actualiza de nuevo hasta obtener una nueva medida.
Esto que parece ser la idea mas lógica y obvia no se me ocurrió hasta tiempo después de estarlo pensando!
28.2.08
Seguimiento exitoso
Después de mucho trabajo arduo y todo eso que se suele decir por fin el filtro ha seguido un objeto correctamente mezclando las dos aproximaciones anteriores, si hay medida usa su esquema estándar de filtro de partículas y cuando no hay medida usa el esquema secundario realimentado.
Durante el tiempo que no tiene medida se va aumentando la incertidumbre linealmente en función del tiempo que ha pasado desde la ultima medida, siendo la incertidumbre inicial la dispersión que se estaba usando en el pf.
Al aumentar la incertidumbre desde la estimación de la realimentación obtenemos un cuadrado en vez de un circulo como cabria esperar para un radio constante, esto se debe a la forma en que está programado.
Usando 150 partículas
El cuadrado que se genera se debe a dos cosas, la primera es que todas las partículas se dispersan desde el mismo centro, la segunda es que todo el área que cubren es equiprobable ya que no tenemos medida.
Usando 10 particulas
Una prueba curiosa es ver como funciona el filtro con tan solo 10 partículas, para mi sorpresa termino encontrando al objeto y siguiéndolo, las fluctuaciones del centroide (cuadrado rojo) mientras no tiene medida son debidas a que se esta calculando el centroide real de las partículas no el estimado debido a la inercia, Como las partículas se dispersan con una función aleatoria normal si usamos muchas partículas ambos centroides convergen, aunque para pocas partículas da un poco de mala pinta.
Suscribirse a:
Entradas (Atom)